Formato de Planeación flexible (Modalidad distancia) Institución Educativa Nicolás Gaviria
Docente: Maria Dolly Tuberquia Usuga Área/Asignatura: Matemáticas
(estadística)
Grado: 7
Grupo: A Semana N°: 8 Fechas
de desarrollo: del 18 al 28 de agosto de 2020
TEMA A TRABAJAR: Interpretación
medidas de tendencia central (moda, mediana y media)
PROGRAMACIÓN DE
ACTIVIDADES
1. ACTIVIDAD INICIAL: Lee con atención
La media o
promedio: La media aritmética es el
valor obtenido por la suma de todos sus valores dividida entre el número de
sumandos.
La mediana: Es el valor que se ubica en el centro de una
distribución. El valor central de un conjunto de valores ordenados en forma
creciente o decreciente.
La moda: Es el valor que se presenta con mayor frecuencia en
una distribución, es decir, el valor que más se repite
2. ACTIVIDAD DE DESARROLLO TEMÁTICO: Observa los ejemplos
PROMEDIO O MEDIA ARITMETICA.
Ejemplo: se pregunta a un grupo de personas sobre la edad y se
obtienen los siguientes resultados:
17, 18, 19, 20, 21, 22, 23.
Se
Interpreta diciendo que la edad promedio es de 20 años.
MEDIANA
Ejemplo: se pregunta a un grupo de personas sobre la edad y se
obtienen los siguientes resultados:
19, 21, 17, 22, 18, 23, 20
Primero se ordenan los datos de menor a mayor
Se interpreta diciendo que el 50% de las personas es menor o igual a 20 años, también se puede decir que el 50% de las personas tiene una edad mayor a 20 años.
Cuando hay una distribución con un número par de casos,(n es par) la mediana es
el promedio de los dos valores medios. Así, en la siguiente distribución: 78,
95, 86, 73, 52, 90, 89, 84, 76, 92
Primero al ordenar la distribución de menor a mayor queda:
Siendo 10 el total de datos, los que aparecen en la posición quinta y sexta están en la mitad de la distribución, entonces la mediana será:
Este resultado indica que el 50% de los valores más bajos tienen un valor máximo de 85.
MODA
Ejemplo:
se pregunta a un grupo de personas
sobre la edad y se obtienen los siguientes resultados:
17, 19,
21, 17, 22,
18, 23, 20,
17, 16.
Se
interpreta diciendo que la edad con más
frecuencia es 17 años.
Otros ejemplos
Los
siguientes datos representan el tiempo (en minutos) que se toman cada uno de
los nueve empleados de una entidad financiera en atender a un cliente 1,
3, 2,
2, 3, 4,
2, 1, 3.
a.
Cuál
es la moda? = 2 y 3 los datos son
bimodales.
La frecuencia con la que atienden los empleados a sus clientes es de 2 o 3 minutos
Cuál es la media?
El tiempo
promedio de atención es de 2 minutos por cliente.
b.
Cuál
es la mediana?
Para calcular la mediana primero se ordenan los datos de menor a mayor:
Se halla el valor ubicado en el centro de los datos Me = 2
El 50% de
los empleados que menos tiempo gastan en atender a los clientes tienen un
tiempo máximo de 2 minutos.
Se puede interpretar
también: el 50% de los empleados que más tiempo gastan en atender a los
clientes tienen un tiempo mínimo de 2 minutos.
En síntesis el ejemplo
anterior queda asi.
Para más información observa el siguiente vídeo
3. ACTIVIDAD DE EVALUACIÓN: Resuelve en tu cuaderno.
1. Se han tomado como muestra las medidas de ocho cables
usados en un arnés para lavadora, las cuales son; 15.1, 15.0,
15.3, 15.2, 15.3,
15.8, 15.4, 15.3
Determine las medidas de tendencia
central (la moda, la mediana y la media aritmética) e interprete cada una
2. Claudia escribió en el tablero un ejercicio para que
los estudiantes de octavo lo resolvieran. Observe los minutos que gastó cada
uno en resolverlo de manera correcta. Clase:
2, 2, 3, 1, 3,
2, 5, 4, 2, 1, 2, 3,
4, 5, 4, 2,
4, 3, 4.
Determine las medidas de tendencia central (la moda, la mediana y la media aritmética) e interprete cada una
3. Las calificaciones de 36 alumnos
en Matemáticas han sido las siguientes: 5, 2, 4, 9, 7, 4, 5, 6, 5, 7, 7, 5, 5,
8, 2, 10, 5, 6, 10, 4, 7, 6, 7, 3, 5, 6, 9, 6, 1, 4, 6, 3, 5, 5, 6, 7.
Determine las medidas de tendencia central (la moda, la mediana y la media aritmética) e interprete cada una
RECOMENDACIONES GENERALES:
·
Enviar las evidencias
a mi whatsapp 313 717 80 09 o al correo tareasieng2013@gmail.com
Muchos
éxitos

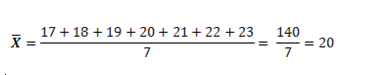


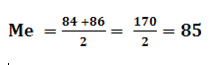



No hay comentarios.:
Publicar un comentario